Describe P Using Polar Coordinates Where R 0 Theta 0
All we have to do is take the values of. A rose curve is a sinusoidal curve graphed in polar coordinates.

Polar Coordinates Ppt Download
θ arctan y x We know.

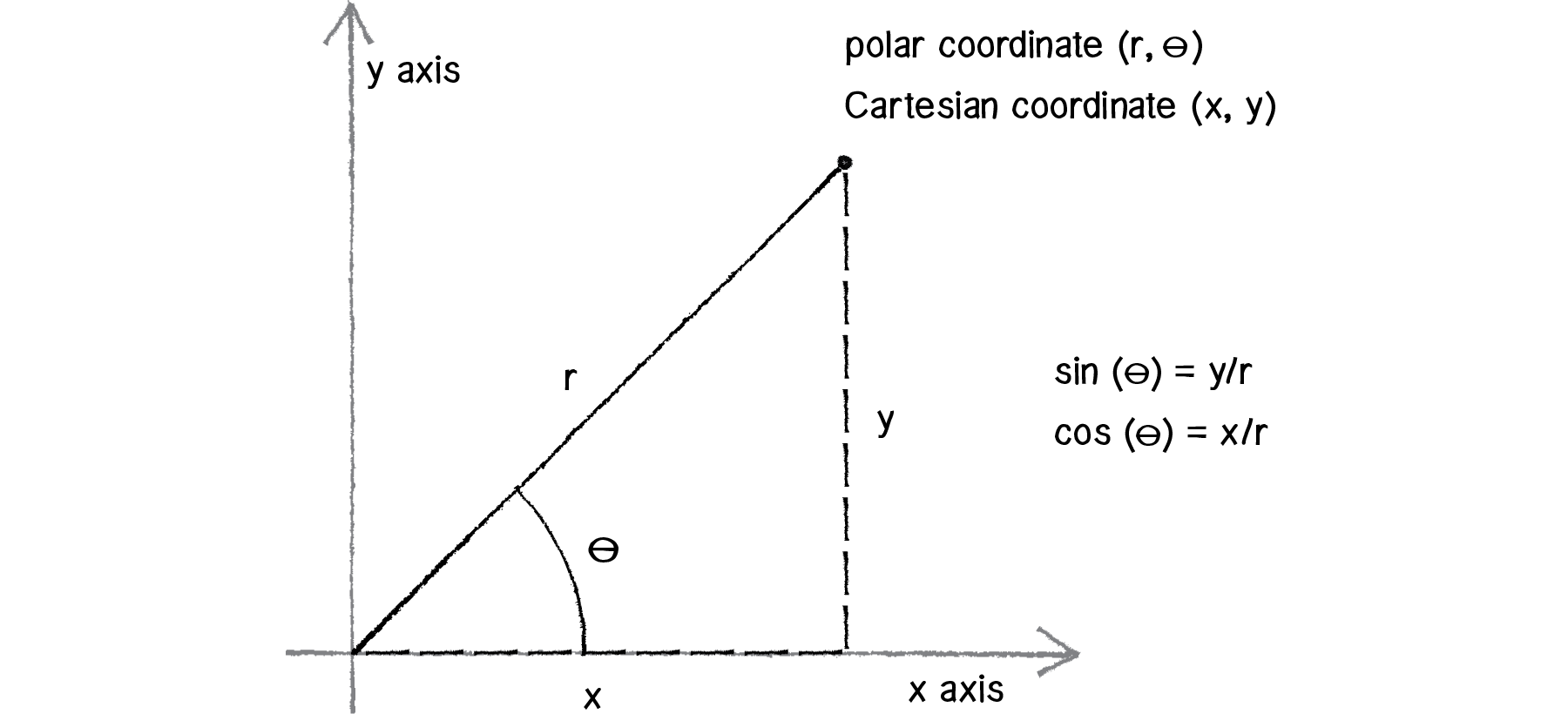
. X r c o s θ. Y r s i n θ. The 3d-polar coordinate can be written as r Φ θ.
In this section we are looking to integrate over polar rectangles. If x. Nevertheless we can solve this if wed like using the equations.
If ris negative P is at a distance jrjfrom the pole on the ray directly opposite the ray of angle that is on the ray of angle ˇ. Xrcos theta x r cosθ. Because the velocity changes direction the object has a nonzero acceleration.
If x 0 ˇ2 if y0 and ˇ2 if y. Pi6. We know polar coordinates is r θ where.
I encountered a question which asked me to describe the rose petal sketched below in polar coordinates. Add 10y k2 to both sides. That makes sense to me for the right petal.
Describe the region D in polar coordinates. Yrsin theta y r sinθ. 0 le theta le 2pi 0 le r le 2endarray These are.
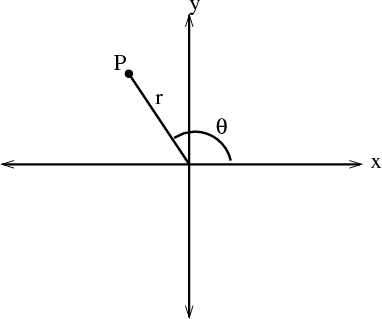
And the pair rand are called the polar coordinates of P. Where are squared is equal to r squared is equal to x squared. In polar coordinates the shape we work with is a polar rectangle whose sides have constant r r-values andor constant θ θ-values.
As r ranges from 0 to infinity and θ ranges from 0 to 2π the point P specified by the polar coordinates r θ covers every point in the plane. R r theta. In this section we want to look at some regions that are much easier to describe in terms of polar coordinates.
R r θ. To convert polar coordinates to rectangular coordinates well use the conversion formulas. Coordinates 11 in terms of polar coordinates.
0 lessthanorequalto r lessthanorequalto 2 sin 9 theta 0 lessthanorequalto theta lessthanorequalto pi R r theta. 2. 0 r rR rr R T TT nt.
For what values of theta on the polar curve rtheta 0. Answered 2021-08-06 Author has 30904 answers. R2 10rsinθ Substitute r2 x2 y2 and rsinθ y.
Here R distance of from the origin. Use polar coordinates to describe the region shown. I have a spherical rendering where the spherical coordinates phi and theta are represented by the x and y axis of the image similar to how world maps work.
0 lessthanorequalto r lessthanorequalto 9 cos 2 theta 0 lessthanorequalto theta lessthanorequalto pi R r theta. This means we can describe a polar rectangle as in Figure 528a with R r θ a r b α θ β. D x y 0 y 6 0 x 6 y y 2 r θ 0 r ______ ______ θ _______.
0. Given any Cartesian coordinates xy there are polar coordinates r theta with -pi2 theta. Find the mass of the triangular region with vertices 0 0 2 0 and 0 1 with density function p x y x2 y2.
Polar to rectangular. Y r sin θ. H 0 un on.
Who are the experts. R cos 3 θ rcos 3theta r cos3θ The general form equation of a rose curve is. Calculus questions and answers.
Thus one possible answer is 2π 4. R r θ a r b α θ β. In these cases using Cartesian coordinates could be somewhat cumbersome.
Solution If we choose r to be positive then r p x2 y2 p 12 12 2 tanθ y x 1 Since the point 11 lies in the fourth quadrant we choose θ π 4 or θ 7 π 4. The complete answer is. Radial distance r distance to origin polar angle θ theta angle with respect to polar axis and azimuthal angle φ phi angle of.
Now given a point on the image with the pixel coordinates pphi theta I want to calculate the average color of all the neighboring pixels on the sphere within a radius radius could maybe more. This is the graph in polar coordinates. Experts are tested by Chegg as specialists in their subject area.
Spherical coordinates r θ φ as commonly used in physics ISO 80000-22019 convention. R2 02 02. Now the polar to rectangular equation calculator substitute the value of r and θ.
Y r sin θ. 3d polar coordinates or spherical coordinates will have three parameters. In each case Pis denoted r.
Well this coordinate point is the origin of both the Cartesian and polar coordinate planes so the polar form is also 00. Cartesian to Polar Coordinates. Adding 2π to θ brings us back to the same point so if we allowed θ to range over an interval larger than 2π each point would have multiple polar coordinates.
However we can still rotate around the system by any angle we want and so the coordinates of the originpole are 0θ 0 θ. These kinds of curves have a flower shape and the loops of these curves are called petals. Another is 27 π 4.
2. 0 r 6 cos 3θ 0 θ π. R2 x2 y2.
The conversion formula is used by the polar to Cartesian equation calculator as. X r cos θ. Though the magnitude of the velocity is a constant the direction of it is constantly varying.
X2 y2 10y k2 k2 1 Matching the right side of the pattern y k2 y2 2ky k2 with y2 10y k2. Because we arent actually moving away from the originpole we know that r 0 r 0. X r cos.
The solution is given as. Distance from the origin and two angles. R r a r T T T T Therefore an object traveling in a circular orbit with a constant speed is always accelerating towards the center.
Given point p on graph. We observe that the following equation will allow us to determine the value of k. From coordinates system point is on 11 x 1 and y 1 on point P.
X r cos θ. Finding r and θ using x and y. Why then it has Polar coordinates are theta.
Multiply both sides by r. To convert from Cartesian coordinates to polar coordinates one can use r p x2 y2 and tan 1yx if x. In polar coordinates the origin is often called the pole.
The rectangular coordinates are called the Cartesian coordinate which is of the form x y whereas the polar coordinate is in the form of r θ. To convert from polar coordinates to Cartesian coordinates xy one can use the formulas x rcos and y rsin. Is on the circle of.
I am given this region and am asked to describe it in polar coordinates. For instance we might have a region that is a disk ring or a portion of a disk or ring. X2 y2 10y.
R a cos k θ racos ktheta r acoskθ where. Plus why squared and tan zeta is equal to so tan Data is equal to why over X um And these air useful for Kurt converting rectangular coordinates A swell into polar coordinates because you can directly plug in our uh and data by.
Polar Coordinates Article Khan Academy

Worked Example Differentiating Polar Functions Video Khan Academy

Solved Find Two Other Pair Coordinates Of The Given Polar Chegg Com

Polar Coordinates Ppt Download
Polar Coordinates Math Insight

Example Identify 4 Possible Polar Coordinates For A Point Using Degrees Youtube

Solved Examiple 7 23 Polar Coordinates For A Chegg Com
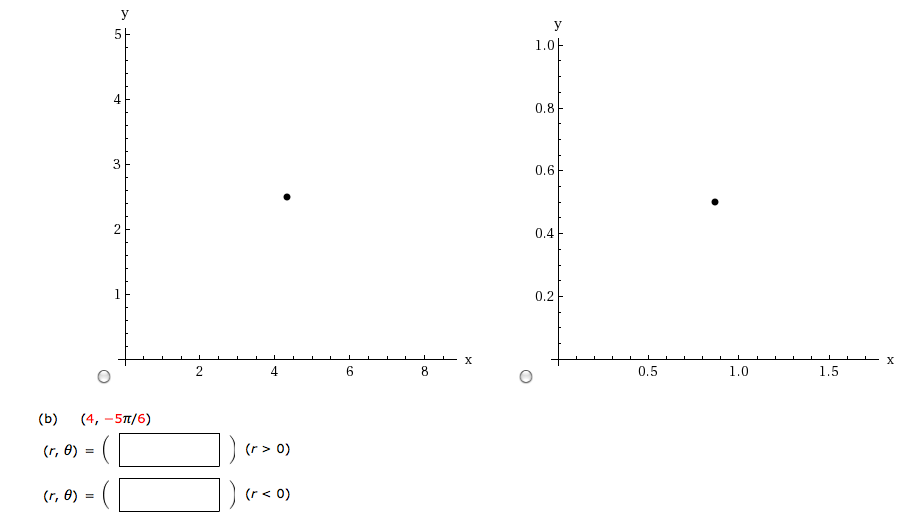
Solved Find Two Other Pair Coordinates Of The Given Polar Chegg Com

Solved Problem 1 4 Pts Hyperbolic Coordinates The Polar Chegg Com

The Spherical Coordinate System Where 8 0 P Is The Polar Angle Download Scientific Diagram

The Polar Coordinate System Boundless Algebra

Polar Coordinates Graphs Algebra And Trigonometry

Find Two Other Pairs Of Polar Coordinates Of The Given Polar Coordinate One With R Homeworklib

6 4 Polar Coordinates Mathematics Libretexts

Find Other Polar Coordinates 8 1 Youtube

Calculus 2 Polar Coordinates 5 Of 38 Graph R 1 Sin Theta Youtube

Comments
Post a Comment